A coil is fitted with series taps such that each tap can be closed by a link, or by a small resistance, as shown below.

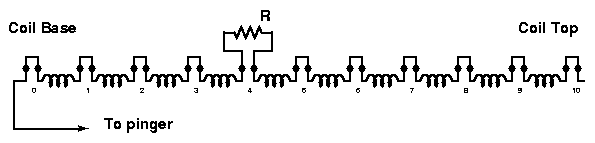
In this example the coil winding is broken into ten roughly equal sections, giving eleven tapping points numbered 0..10 from the base.

A resistance is inserted into each tap, one at a time, and the resulting Q measured for each of the eleven taps. An additional Q measurement is taken with no resistance inserted. The current profile can then be calculated from the resulting set of twelve Q measurements.

This method does not require knowledge of the resistor value, or the resonant frequencies. No voltage or current measurements are required.

The calculation proceeds as follows: For the ringdown, for each frequency component,

  Eloss/Es = 2 pi / Q

where E_loss is energy lost per cycle and E_s is the stored energy, (both functions of time).

Consider E_loss to be the sum of the energy lost in the coil (E_c) plus the energy lost in the extra series resistance (E_x). Then we can say

 Ec/Es = 2*pi/Qs                  ...(1)

where Q_s is the Q measured without the extra resistor. With the resistor added at point x = 0..10 in the coil, we have

 (Ec + Ex)/Es = 2*pi/Qx           ...(2)

where Q_x is the associated observed Q. We have 11 of these equations.

Substituting (1) into (2) gives

 Ex/Es = 2*pi/(1/Qx - 1/Qs)       ...(3)

Now at any cycle of the ringdown,

 Es = Lee * Ib^2/2

where I_b is the peak base current, and the 11 equations

 Ex = R * Ix^2/(2*f)   x = 0..10

in which I_x is the peak current at the resistor point x,

With these, (3) becomes

 Ix^2/Ib^2 = 2*pi*f*Lee/R * (1/Qx - 1/Qs)

which is independent of time now that we have eliminated all the energy terms. Noting that I_b = I_x when x = 0, we have

 1 = 2*pi*f*Lee/R * (1/Q0 - 1/Qs)

and the other ten equations

 Ix^2/Ib^2 = 2*pi*f*Lee/R * (1/Qx - 1/Qs) ; x = 2..10

The first equation gives

 2*pi*f*Lee/R = Q1 * Qs/(Qs - Q0)

and using this to eliminate all the unknowns in the remaining ten equations gives

 Ix^2/Ib^2 =  (1/Qx - 1/Qs) * Q0 * Qs/(Qs - Q0) ; x = 1..10

Therefore eleven Q measurements Q₀ to Q₁₀, one for each link, plus an extra one Q_s of the coil without the resistor, can be used to determine the current profile I_x/I_b through the formula

 Ix/Ib = 1  ; x = 0
 Ix/Ib = sqrt{ (Qs - Qx)/(Qs - Q0) * Q0/Qx } ;  x = 1..10

It can be seen from the above equation that the resulting current profiles are quite sensitive to the difference between measured Q values. Therefore, for this method to be successful, high precision Q measurements are necessary.

Purpose

(a) To determine whether computer analysis of base current ringdown waveforms provides a sufficiently accurate method for determining current profiles.

and

(b) To confirm the predicted current profile for the coil, and to demonstrate the elevated current maximum in a resonating solenoid, as shown in fig 6.1 of pn2511.

Test Coil

Terry Fritz has constructed a test coil for this experiment, Test Coil. This coil has a h/d ratio of 0.9, which is ideal for demonstrating the current maximum induced through the internal capacitance of the coil.

The tssp model produces the following predictions for the coil

          Measured      Modeled       Error
f1/4      229.9 kHz     229.3 kHz     -0.3%
f3/4      578.1 kHz     570.4 kHz     -1.3%
f5/4      904.1 kHz     908.9 kHz     +0.5%
Ldc        39.0 mH       39.18 mH     +0.5%
Rdc        32.65 ohms    32.91 ohms   +0.8%

The modeling program is making a rough compensation for the coil former dielectric in the above figures. The frequency match is good on the first three resonant modes, which is enough to indicate that the model is correctly set up. Therefore we expect a good match on the current profiles.

Measurements

By using an inserted resistance of 100 ohms, with Q measurements made by base current waveform capture and analysis by tcma, the following set of Q readings were obtained, shown along with their calculated I_x/I_b values:

Turn   Measurement      Q1/4   Ix/Ib    Q3/4  Ix/Ib      Q5/4  Ix/Ib

0     Q0  TEK00001      283.73 1.000   167.37 1.000     102.28 1.000
43    Q1  TEK00002      234.04 1.243   134.53 1.907      87.25 2.308
87    Q2  TEK00003      219.97 1.320   135.33 1.886      98.32 1.418
135   Q3  TEK00004      215.22 1.347   152.51 1.432     105.97 0.354
179   Q4  TEK00005      216.63 1.339   176.59 0.661      91.38 1.999
222   Q5  TEK00006      225.62 1.288   182.10 0.356      83.81 2.557
265   Q6  TEK00007      242.45 1.198   161.33 1.185      94.60 1.743
309   Q7  TEK00008      268.92 1.068   138.21 1.810     105.66 0.443
354   Q8  TEK00009      309.45 0.887   129.02 2.051      95.48 1.670
398   Q9  TEK00010      366.75 0.648   141.24 1.731      87.35 2.301
442   Q10 TEK00011      464.28 0.060   184.04 0.149     107.05 0.000

along with the unloaded reading

      Qs  TEK00000      465.35         184.46           106.52

The detailed tcma output results from which these results are summarised, can be seen in tcma-output.txt. Raw data CSV files, and pictures of the experiment can be seen here. The measurement run only took a few minutes, so we make no attempt to compensate for the negligible temperature variation.

Results

When plotted against the predicted current profile for each resonant mode, we obtain
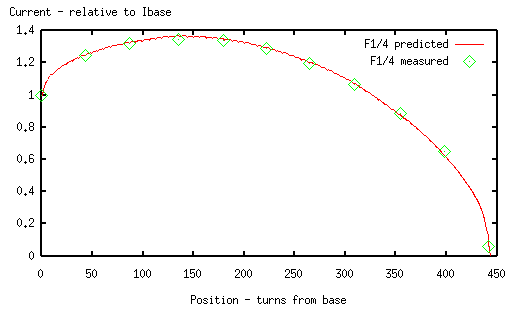1/4 wave
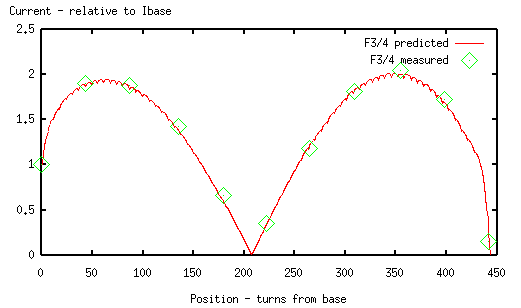3/4 wave
We see good agreement on the 1/4 wave mode, and a reasonably good match with the 3/4 wave. The 5/4 wave mode below is showing some significant errors, of up to 10%.
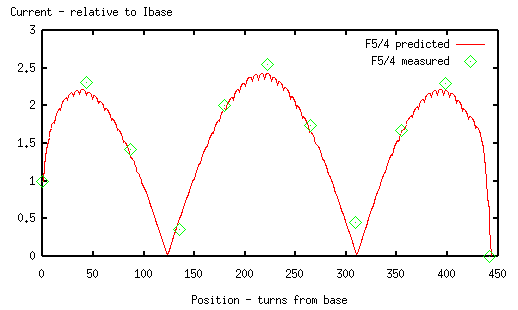5/4 wave
Note: The ripple effect on the predicted current profiles is an artifact of the coil modeling software. It is caused by the interpolation method which deals with the limited spatial resolution of the internal capacitance. The particular method used has good global accuracy at the expense of some local aliasing noise, which appears as the ripple. This turns out to be quite convenient in practice, because you can see at a glance those parts of the current profile which are being strongly affected by internal capacitance.

(a) Q Measurements

The Q determination appears to be sufficiently precise for accurate measurement of the current profiles of the lowest resonant frequency. Errors of around 3% occur with the 3/4 wave profile, and around 10% with the 5/4 wave. This is partly due to limitation of the modeling program, and partly due to sensitivity of the calculation to the small differences between Q measurements, especially at low currents. For all three modes, the discrepancies between measured and predicted current profiles are comfortably within the combined errors of the measurement and modeling processes.

(b) Elevated Current Maximum

This feature of solenoid resonance, which results from the effect of mutual capacitance between one part of the coil and another, is one of the main departures from the kind of transmission line behaviour described by the familiar telegraphist's equation. The elevated current maximum is clearly demonstrated in the 1/4 wave profile.

The experiment also gives us a clear demonstration that the ratio Les/Ldc can exceed unity, in this case by around 12%.

We can also extract a direct measurement of the equivalent energy storage inductance, L_ee from the results as follows: If R_in is the input resistance at resonance, and R is the added series resistance, we have

   Rin = 2 pi F Lee/Qs

and

   Rin + R = 2 pi F Lee/Q0

Rearranging these and substituting to eliminate the unknown R_in, we obtain

   Lee = Q0 Qs R / (Qs - Q0) / (2 pi F)

Using the measured values of R, Q₀, Q_s, and F, we get

         F       R     Q0     Qs     Lee Meas   Lee Model      Error
f1/4  229900  100.57  283.73 465.35   50.6 mH    50.87 mH      +0.5%      
f3/4  578100  100.57  167.37 184.46   50.0 mH    49.98 mH       0.0%
f5/4  904100  100.57  102.28 106.52   45.5 mH    39.95 mH     -12.2%

which confirms the predicted values of L_ee at f1/4 and f3/4. The error at f5/4 is due to the closeness of the two Q readings, each of which is subject to a few percent error. An accurate value for L_ee at this resonance would require re-measuring with a higher value of series resistance.

This experiment provides strong evidence that the modeling process is correctly quantifying the internal capacitance of the coil, and that this capacitance is being properly applied in the solenoid model.