| TSSP: Tesla Coil Mode Analyser |
A method for precision measurements of resonant frequency, Q factor, input impedance, energy storage inductance, and coupling
coefficients.
Updated: 12 Apr 2012
When a solenoid is struck into resonance by means of a sharp transient,
the base current contains the full spectrum of mode frequencies, with
each component undergoing an exponential ringdown according to its own
particular Q factor. The base current waveform can be captured by a
digital scope and the resulting data can be analysed by software to
extract the mode frequencies and their Q factors.
With reasonably clean waveforms captured by the scope, a repeatable
accuracy of 0.01% on frequency and 0.1% on Q factor can be readily
achieved. This method has the following advantages over more traditional
methods of Q measurement:
- No absolute analogue measurements are involved - the method requires a linear but relative amplitude sensitivity of the scope.
- Frequencies and Q factors of several resonant modes can be measured simultaneously.
- More than one coil can be measured simultaneously.
- By using the base current, the measurement has minimal impact on the measured coil itself.
- Conducive to automated unattended measurements.
- Very simple to set up.
- The actual error on each individual measurement is available.
The remainder of this document describes the measurement circuit and procedure, the analysis software, and we show examples
of some of the applications for this technique.
An effective test setup, which we call a pinger, was devised by Terry Fritz and is shown below.
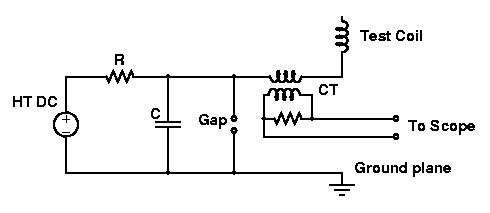
C around 27nF, R around 10Megohm. Supply circa 2.5 kV, Victoreen gap, Pearson CT.
Both the capacitance C, and the coil's DC capacitance Cdc, are charged
up towards the supply voltage V via the resistance R. At some point the
spark gap fires, thus placing a negative going step voltage transient onto
the coil base, and the coil is excited with a total energy approaching
0.5 * Cdc * V2. The reservoir capacitance C provides a
sufficient background current to ensure that the gap stays conducting
at low resistance during the subsequent ringdown. The ping repetition
rate is determined by the RC time constant.
The resistance across the CT output terminals should be chosen to match the
specified output impedance of the CT.
The test setup is not sensitive to stray reactances introduced into the
base circuit by the pinger, and therefore layout is not at all critical.
However, for best results, care should be taken not to introduce any
significant extra series resistance into the coil base circuit.
Waveforms should be captured with a small amount of pre-trigger to
ensure that the front of the event is acquired. Care should be taken
to ensure that at no point does the signal become clipped in the scope Y
amplifier. Timebase should be chosen so that the highest mode of interest
is represented by at least 2 or 3 samples per cycle. For best results the
captured trace should be averaged over say 128 shots of the ping circuit.
The resulting waveform has a typical spectrum
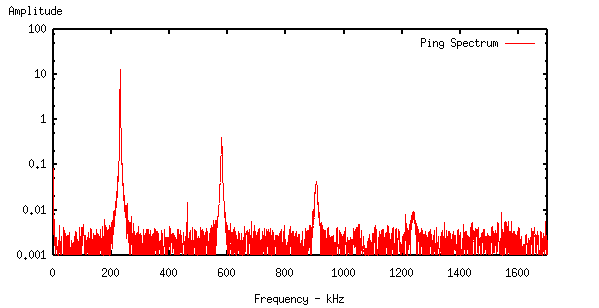
We see the lowest four resonant modes of the coil - further modes are
obscured by the noise floor, the level of which is set by the quantisation
noise due to the scope trace digitisation.
The maximum possible accuracy of the subsequent Q and F extraction is limited by the information content of the captured
trace, such that the errors are at best
Q Error = 100 / sqrt( NY * NT) percent
F Error = 100 / NT percent
for each component mode, where
NY is the number of Y-axis quantisation steps spanned by the particular mode,
NT is the number of T-axis steps spanned by the ringdown.
NY should be maximised by turning up the Y gain as far as possible without
clipping occuring. NT should be maximised by using the shortest possible
time step consistent with capturing the whole or most of the ringdown.
Typical values are NY=400, NT=8000, giving an accuracy of 0.06% on Q
and 0.01% on F, in the absence of noise. Random trace noise, which can
be easily reduced by averaging over many pings, will degrade the actual
accuracy below these theoretical limits. In practice, the theoretical
accuracy can be approached quite closely when using say 128 pings
per trace.
Waveform data should be stored as a two-column ASCII data file with
either a comma or a space separating the two fields. The program will
accept either DOS or UNIX line terminators. The first column should be
the time step, in seconds, and the second column should be the relative
current amplitude. The time interval between steps should be uniform.
The program will ignore any frequency components below 30kHz.
The example waveform above, which consists of a 16-ping average, when analysed gives the following output:
PK FREQ kHz (Error +/-) Q FACTOR (Error +/-) LEVEL
1 229.956 (0.01%,21Hz) 465.35 (0.12%, 0.6) -0.1dB
2 578.100 (0.01%,53Hz) 184.46 (1.43%, 2.6) -17.3dB
3 904.162 (0.01%,83Hz) 106.52 (14.33%,15.3) -24.6dB
4 1237.308 (0.01%,113Hz) 73.92 (107.4%,79.4) -30.3dB
Accounted for 99.84% of input signal
In this example, the deterioration of Q determination with higher modes
is almost entirely due to Y axis quantisation noise and the extraction
is working close to the theoretical limits.
Downloading and Compiling
The source code for the program (current version: 0.1g) can be download
from tcma.c and compiled according to your local
C compiling conventions. A typical compiler command would be
cc -o tcma tcma.c -lm
and you will benefit from turning on full optimisation.
The program will use up to
5 Mbytes or so of RAM, depending on how much work it is told to do.
Running the program
Run the program by feeding the waveform datafile into the program's standard input, eg
./tcma < TEK00001.CSV
and the results and progress messages go the the stderr stream. By default, the program will go to work on the strongest
four components found in the input file. This behaviour can be controlled by specifying the number of peaks to look at on the
command line, eg
./tcma -npeaks 12 < TEK00001.CSV
will generate output for the strongest 12 peaks. Analysis of a particular peak can be selected with
./tcma -peak 5 < TEK00001.CSV
which will report results for only the 5th strongest peak in the input file. You can find out what signals the
program has detected by using
./tcma -signals < TEK00001.CSV
which will make tcma print out approximate frequency values, but not go on to analyse them in detail.
The program is able to make an estimate of what the final accuracy of each F and Q result actually is, and these
are printed as +/- limits following each value.
The LEVEL column shown in the results indicates the total RMS signal level of each mode,
taken over the whole ping event.
The stdout stream is
reserved for various other optional functions of the program. For example, the fourier transform (FT) of
the input waveform can be generated by
./tcma -ft < TEK00001.CSV > tek00001.ft.csv
which generates a two column FT datafile.
Inspection of the code will reveal a number of other command line options which are used only for program testing.
These are not yet documented.
How it Works
The program works by synthesizing a waveform with the equation
V = A1 sin( 2 pi F1 t + P1) exp( -pi F1t/Q1)
+ A2 sin( 2 pi F2 t + P2) exp( -pi F2t/Q2)
+ ...
+ An sin( 2 pi Fn t + Pn) exp( -pi Fnt/Qn)
in which
Aj is the amplitude,
Fj is the frequency,
Qj is the Q-factor,
and Pj is the phase,
of the jth component,
and n is the highest component number under consideration.
Initial values for the parameters are estimated from a fourier transform
of the waveform, and then the parameters are systematically and
deterministically refined to minimise the error when compared with the
captured scope trace. To avoid the computationally intensive problem of
optimising 4n parameters simultaneously, the program applies a
narrow band filter to the waveform so that it can obtain a match on each
component separately. The band-limited exponential ringdown waveshape
is highly modified by the filtering process, so the program must apply
the same narrow band filter to the synthesized waveform before making
comparison. By this means, only 4 parameters need be matched
simultaneously.
As a further optimisation, the program uses a set of three different
correlation functions, each of which is sensitive separately to
F, Q, or P errors, and each of which is
insensitive to overall amplitude A. Thus three parameters of
each mode can be refined more or less independently, and the amplitude
coefficient A is determined at the end by a standard correlation
function.
The actual error in any particular measurement is determined by
constructing a second synthesized version of the waveform but with slight
errors in the parameters. This synthesised waveform is compared with
the waveform that was synthesized to match the input trace, and the
artificial error is adjusted to achieve the same values of the three
correlation functions that the original synthesized waveform has when
compared with the input signal.
An estimate of overall signal quality is given at the end by synthesizing
the whole waveform and subtracting this from the input signal, without
any filtering. The total amount of input signal accounted for in this
way is indicated as a final percentage.
Single Resonator Q Variations
High Q factor is of crucial concern to the CW coiler, and tcma
can be used as an investigative tool to track down sources of dissipation
in the coil. The effect of changes to toploads, ground arrangements, etc,
can be accurately and repeatably assessed. By a careful and thoughtful
process of elimination, it should be possible to construct an energy loss
budget for a given resonator, although this has not yet been achieved.
Gap and Proximity Losses
The program may also be of use in investigating the relative importance
of gap loss and proximity loss in traditional TC primary windings. There
is evidence that both these factors may be significantly involved in
setting the overall efficiency, but the choice of optimum primary design
requires a trade-off between the two. Therefore it would be helpful to
know the relative contribution of these two sources of loss. tcma
may provide a useful tool for this kind of investigation.
Coupled Resonators
The program is able to analyse the beat envelope of a
traditional Tesla coil. An example waveform from such a coil (tfss270501) has the spectrum
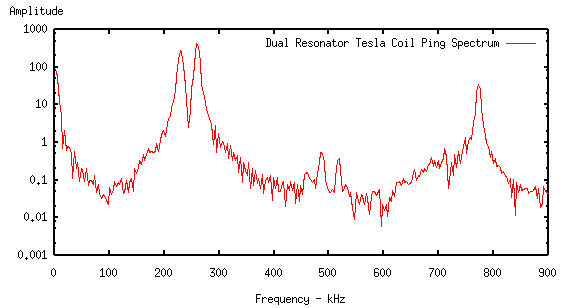
and tcma reports the following for the two strongest component signals,
PK FREQ kHz (Error +/-) Q FACTOR (Error +/-) LEVEL
1 257.060 (0.49%,1252Hz) 101.50 (6.98%, 7.1) -1.7dB
2 226.677 (0.21%,465Hz) 54.19 (5.23%, 2.8) -4.8dB
Accounted for 98.96% of input signal
The closeness of the two modes has reduced the accuracy of the individual
Q determinations, but further work on tcma will resolve this problem.
The program should eventually able to supply the essential information
from which accurate values of the effective coupling coefficient can
be determined.
Multiple Coils
More than one coil can be pinged at a time, by simply connecting their
bases together. The low resistance of the spark gap (relative to coil
base impedance) ensures that the coils are not mutually coupled through
the ping circuit. An example FT for a two-coil ping is shown below,
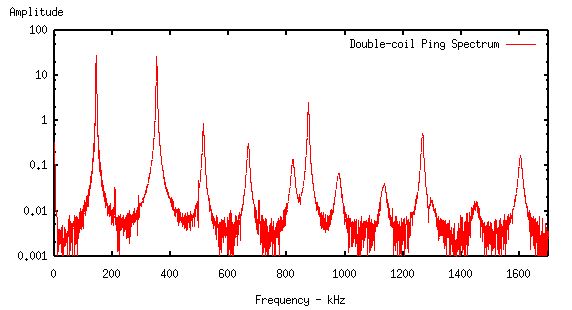
and the tcma output for this waveform is,
PK FREQ kHz (Error +/-) Q FACTOR (Error +/-) LEVEL
1 351.208 (0.01%,29Hz) 216.04 (1.65%, 3.6) -2.0dB
2 143.476 (0.06%,93Hz) 241.10 (0.11%, 0.3) -4.9dB
3 873.002 (0.01%,71Hz) 243.24 (0.45%, 1.1) -16.7dB
4 511.845 (0.01%,42Hz) 112.90 (1.43%, 1.6) -23.8dB
5 1265.541 (0.01%,103Hz) 191.11 (3.92%, 7.5) -22.8dB
6 666.399 (0.01%,54Hz) 91.25 (1.65%, 1.5) -27.7dB
7 1602.539 (0.01%,131Hz) 138.07 (6.98%, 9.6) -26.1dB
8 819.766 (0.01%,67Hz) 78.88 (6.98%, 5.5) -28.4dB
9 977.371 (0.01%,80Hz) 67.92 (9.31%, 6.3) -32.8dB
10 1911.548 (0.01%,156Hz) 105.95 (14.33%,15.2) -28.9dB
11 1133.085 (0.01%,93Hz) 61.56 (16.55%,10.2) -33.3dB
Accounted for 93.63% of input signal
The poor error of the first peak at 351kHz is due to the collision of the
1/4 wave mode of one coil, and the 3/4 wave mode of the other coil, which
happen to be within 2kHz of one another. tcma has locked onto
the strongest component, but the Q extraction is upset by the presence of
the other signal. Therefore, this method may only give useful results
when the coils involved have suitably distinct resonances. Ideally,
each component frequency should be more that 6% away from any other.
Current Profiling
This method can be used to accurately determine the current profile of
a suitably modified coil, by means of a resistance insertion method.
The method requires high precision Q measurements, and tcma,
along with the pinger circuit, works very well in this application. See tfcp260302 for an experiment which employs
this technique.
Base Input Resistance, Energy Storage Inductance
Both of these can be measured to high precision using tcma,
the pinger circuit, and an additional resistance. The Q of the coil is
measured twice, once with a known resistance R inserted into
the base circuit to give the loaded Q factor Qr,
and again without the extra resistance, giving the unloaded Q factor
Qu. The resistance should be chosen so that
Qr is less than half that of Qu.
From these measurements, we can calculate
Rin = Qr R / (Qu - Qr)
Lee = Qr Qu R / (Qu - Qr) / (2 pi F)
for each resonant frequency in the ping waveform.
Output Admittance, Energy Storage Capacitance
A similar procedure to the above can be carried out to obtain the
output admittance and the energy storage capacitance, by applying a
known shunt loading resistance between the top of the coil and ground.
This is inevitably a less accurate measurement, due to the sensitivity
of the resonator to stray reactances applied to the coil top.
Soundcard Capture
The plan is to extend tcma so that it can work from a waveform
captured by a PC soundcard. This would normally require a frequency
translation of the base current signal before it can be applied to
the soundcard input, which means that the program could in most cases
only analyse one resonant mode at a time, and this would be at reduced
accuracy. Nevertheless, it may be possible to obtain useful results and
in view of the fact that more coilers possess soundcards than digital
scopes, the approach may be more widely usable.
K-factor Extraction
The present version of the program is severely limited in its ability to
separate closely spaced resonant modes, which limits the dual resonator
analysis to situations involving fairly high coupling coefficients.
At low k factor the program cannot separate the two modes sufficiently to
match each one separately, and it is therefore necessary to iteratively
match both simultaneously. It is hoped that eventually it will be
possible to compare k factors measured at the resonant frequencies with
the k factor determined from low frequency mutual inductance measurements.
Many thanks to Terry Fritz for providing the high quality scope waveforms used in the above examples.
Maintainer Paul Nicholson, paul@abelian.demon.co.uk.



