Given a secondary resonator with length h carrying a top voltage Vtop, we can say that the average voltage per unit length is Vtop/h.

However, for most secondaries the voltage rise is not uniform and therefore for part of the coil at least, the voltage gradient must exceed this average value.

We can compare the actual highest voltage gradient on the coil with the uniform Vtop/h value by defining a voltage stress factor,

Stress factor = Highest gradient / average gradient

This factor is relevant when calculating the maximum volts per turn or volts per unit length for a coil. Given the energy storage capacitance Cee for a coil, the expected peak top voltage for a primary energy E is

Vtop = sqrt( 2 * E / Cee)

When this voltage is divided by length or turns to get the desired peak gradient, the result should be multiplied by the stress factor to take account of the non-uniform voltage rise. The voltage stress factor varies with the shape of the coil and the size of the topload. This page provides tables and formulae by which the stress factor for a given system can be estimated.

We consider all types of secondary shape: flat, cylinder, and both inverted and upright cone coils. To do so we define two shape parameters A and B to describe each coil:

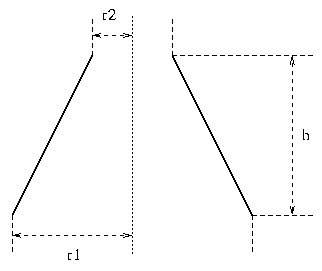
Starting with the definitions shown on the right, in which r1 is the radius across the lower (earthed) end of the coil, and r2 is the radius across the upper (hot) end, we define: A = h/d B = (r1 - r2)/d where h = overall height of the coil. and d = average diameter = r1 + r2. Thus A is the familiar h/d ratio with A=0 corresponding to a flat spiral coil. The factor B describes the tilt of the sides of the coil, and is zero for a cylindrical solenoid. A cone coil which rises to a point at the top has B=1 and an inverted pointed cone balanced on its point has B=-1. Shapes with A=0 range from B=1 corresponding to a full spiral with center hot, to B=-1 corresponding to the full rim-hot spiral. The shape with A=0 and B=0 corresponds to a coil with all the turns bunched into an annular ring, thus sharing a common EMF per turn. For this coil the voltage gradient is therefore uniform and stress factor is unity.

Here we show the voltage stress factors for various shapes of unloaded secondary which were obtained by modeling 1073 coils using Terry Fritz's Sun workstation. About a dozen coils were modeled for each cell, using various sizes, turns, and heights above ground. The average value is shown in the table, along with an indication of the spread of values obtained.

B
A		-1.0	-0.8	-0.5	-0.3	0.0	0.3	0.5	0.8	1.0
	0:	1.77 ±3%	1.58 ±3%	1.34 ±3%	1.21 ±4%	1.0	1.33 ±1%	1.55 ±1%	1.92 ±1%	2.16 ±1%
	1.0:	1.81 ±17%	1.70 ±5%	1.44 ±3%	1.28 ±3%	1.25 ±1%	1.49 ±1%	1.71 ±1%	2.05 ±1%	2.12 ±36%
	1.5:	1.90 ±4%	1.72 ±2%	1.45 ±4%	1.31 ±3%	1.29 ±2%	1.58 ±2%	1.80 ±1%	2.15 ±2%	2.34 ±2%
	2:	1.95 ±3%	1.75 ±2%	1.48 ±3%	1.34 ±4%	1.30 ±0%	1.63 ±2%	1.87 ±1%	2.22 ±1%	2.41 ±1%
	2.5:	1.99 ±4%	1.83 ±6%	1.52 ±4%	1.34 ±4%	1.33 ±3%	1.68 ±1%	1.93 ±1%	2.28 ±1%	2.48 ±1%
	3:	2.00 ±3%	1.82 ±3%	1.51 ±3%	1.33 ±3%	1.35 ±2%	1.72 ±1%	1.99 ±1%	2.33 ±2%	2.53 ±1%
	4:	2.05 ±2%	1.85 ±4%	1.52 ±3%	1.32 ±3%	1.36 ±1%	1.79 ±1%	2.06 ±2%	2.42 ±1%	2.62 ±1%
	6:	2.11 ±5%	1.91 ±5%	1.52 ±2%	1.33 ±2%	1.39 ±1%	1.87 ±1%	2.17 ±1%	2.55 ±1%	2.75 ±1%
	8:	2.13 ±6%	1.89 ±2%	1.54 ±5%	1.34 ±5%	1.41 ±1%	1.92 ±1%	2.24 ±1%	2.63 ±1%	2.83 ±1%
	10:	2.10 ±3%	1.90 ±4%	1.51 ±1%	1.32 ±1%	1.43 ±1%	1.96 ±1%	2.30 ±1%	2.70 ±1%	2.90 ±1%

We can see that cylinder coils generally have the smoothest voltage profiles, with the most uniform gradients being obtained at small h/d. Coils with top diameter slightly wider than the bottom also do quite well at the larger h/d. The table suggests that there is an optimum value of B between -0.5 and 0, which gives the smoothest voltage profile for any given h/d. A coil of that shape could perhaps support a 10% higher voltage than the same length of cylindrical solenoid.

The table above is only valid for unloaded coils because adding a topload modifies the voltage distribution of the coil and therefore the stress factor will alter too. We can accomodate the effect of the topload to a reasonable approximation by the procedure described in this section.

First we define:

Ctop = The capacitance to ground of the in-situ topload.
Ces = The total equivalent shunt capacitance of the toploaded resonator (which includes Ctop).
Les = The equivalent series inductance of the unloaded secondary.
Ldc = The DC inductance of the secondary coil.

Given a toroided coil with base current Ib, we can divide Ib into a component Ib * Ctop/Ces which goes on to form the topload current, ie a 'straight through' uniform current, and the remainder of the base current, Ib * (1 - Ctop/Ces) which is the current that charges up the coil's self capacitance and never reaches the topload.

We can then take the top voltage Vtop to be the sum of the voltages induced separately by each current component, ie

Vtop = w * Ldc * Iu + w * Les * Ic

where w = 2 * pi * Fres is the angular resonant frequency.

Then we can apply the unloaded coil stress table to just the w * Les * Ic component of the top voltage. If T is the relevant stress factor from the table, the highest volts per unit length due to this component would be

T * w * Les * Ic/length     ... volts/metre

and if we assume a uniform gradient for the voltage induced by the uniform topload current, its gradient is

w * Ldc * Iu/length     ... volts/metre

Taking the overall highest gradient to be the sum of these (in the worst case scenario), we obtain the total gradient

Ib * w/length * (T*Les*(Ces-Ctop) + Ldc*Ctop)/Ces     ... Volts/metre

for the combined highest gradient. This is equivalent to an overall stress factor

T' = w^2 * (T*Les*(Ces-Ctop) + Ldc*Ctop)

because the average volts/metre is Ib/(w * Ces * length).

We now let the coil's shunt capacitance be Cxs and approximate it with Ces - Ctop, and noting that

w' = 1/sqrt(Les * Cxs) = the coil's unloaded resonant frequency,
w'' = 1/sqrt(Ldc * Ctop) = the notional resonant frequency of the DC inductance with Ctop.

we arrive at the reasonable approximation

T' = T * (w/w')^2 + (w/w'')^2

for the secondary voltage stress factor of the loaded coil, given the unloaded stress factor T. Of course, the ratios of the angular frequencies w, w', and w'', can be replaced by the ratios of the frequencies in Herz.

As Ctop tends to zero, w tends towards w' and w'' tends towards infinity, so T' tends towards T. For very large toploads, w becomes approximately equal to w'', and w becomes a lot smaller than w', so T' tends to unity.