Examples of voltage and current distribution profiles for Tesla secondary coils.
All the graphs show absolute magnitude of voltage and current when
fed by a zero impedance voltage source into the base. Resonances are
quarter-wave unless otherwise stated. Input is always 1 volt.
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Example 1: Typical coil without toroid |
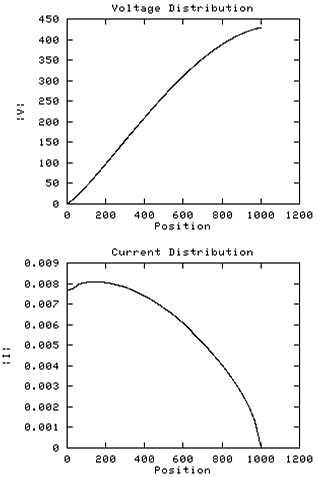 These are the curves for the coil when modeled as accurately as possible,
taking into account the non-uniform capacitance distribution and the
effects of mutual inductance and internal capacitance.
These are the curves for the coil when modeled as accurately as possible,
taking into account the non-uniform capacitance distribution and the
effects of mutual inductance and internal capacitance.
Note the linear rise of V over the lower 70% of the coil, with
a gentle fall of the slope above that. The current is a distorted
cosinusoid, with a peak about 15% up the coil due to displacement
currents in the internal capacitance. Note the slight concavity
in the V profile below the current peak.
In this example Vt is around 454 volts with an input
current Ib of 0.0081 amps. Thus the transimpedance is
around 56K ohms.
| Example 2: With no internal capacitance |
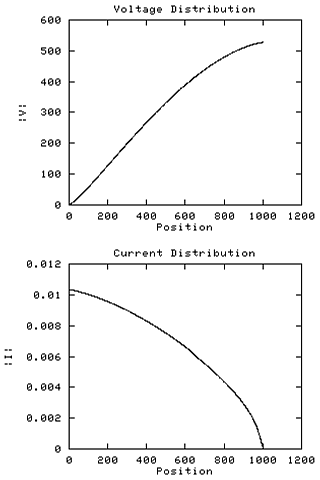 The same coil as above, but with internal capacitance 'switched off'
to demonstrate the effect of Cint on the amplitude profiles.
The resonant frequency went up by 7.4% as a result.
The same coil as above, but with internal capacitance 'switched off'
to demonstrate the effect of Cint on the amplitude profiles.
The resonant frequency went up by 7.4% as a result.
The current
peak at 15% height has disappeared. The V profile, if anything is
slightly more linear without the internal capacitance.
The transimpedance has fallen slightly to around 51K ohms, but is still
quite a bit higher than the cosine based prediction.
Note that the current peak in the lower part of the coil which has disappeared
with the internal capacitance is due to the asymmetric effect of its
displacement currents. Above the midpoint, displacement currents
into the internal capacitance are always in phase with those going into the
external capacitance, whereas below the midpoint the internal displacement
currents are out of phase with those of the external capacitance.
The effect of this asymmetry on the current profile can be visualised
as a removal of current from the top half and a corresponding injection
of current into the lower half. Another way to regard this is as an
increase of the effective capacitance per unit length in the top half, and a
decrease in the lower half.
| Example 3: With no longitudinal coupling |
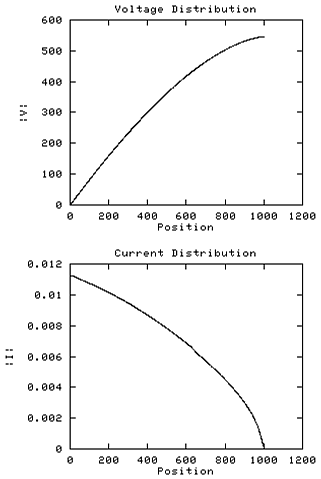 The coil, still with internal capacitance switched off as above but
also the mutual inductance profile has been replaced by an equivalent
uniform self inductance per turn of Ldc/Nt. The
resonant frequency fell by 1% on removal of the mutual inductive
coupling, demonstrating that one of the effect of mutual inductance
is to increase the velocity factor slightly, ie the mutual inductance
'stiffens the spring'. This coil is now operating with no longitudinal
coupling whatsoever.
The coil, still with internal capacitance switched off as above but
also the mutual inductance profile has been replaced by an equivalent
uniform self inductance per turn of Ldc/Nt. The
resonant frequency fell by 1% on removal of the mutual inductive
coupling, demonstrating that one of the effect of mutual inductance
is to increase the velocity factor slightly, ie the mutual inductance
'stiffens the spring'. This coil is now operating with no longitudinal
coupling whatsoever.
The voltage rise is now noticeably less linear without the smoothing effect
of the mutual inductance and is beginning to show the convex slope of a
distorted sine curve. The current profile has hardly changed.
Transimpedance has fallen further to 48K ohms, a change of 3K from the
51K predicted with mutual inductance, suggesting that replacing mutual
inductance with a uniform equivalent self inductance might introduce
an error of around 5%.
| Example 4: With uniform external capacitance |
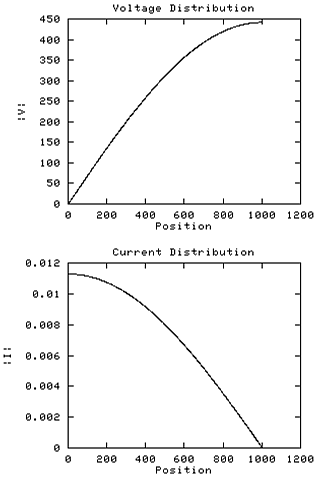 The model shown above without longitudinal coupling is now further
simplified by replacing the non-uniform external capacitance by a
uniform distribution.
The model shown above without longitudinal coupling is now further
simplified by replacing the non-uniform external capacitance by a
uniform distribution.
Both the V and I profiles are now recognisably sinusoidal in shape,
which is unsurprising as this simplified coil now qualifies as a
standard uniform transmission line.
It can perhaps be judged from these charts, and the previous set of
charts, that the two factors acting to linearise the voltage profile
are the smoothing effect of mutual inductive longitudinal coupling,
and the decreasing external capacitance with height. These two
effects compensate for the current reduction occuring towards the
top due to external capacitance.
The transimpedance has fallen further and is now exactly
the value calculated on the basis of a cosine current profile,
ie 4 * F * Ldc.
| Example 5: With exponential external capacitance |
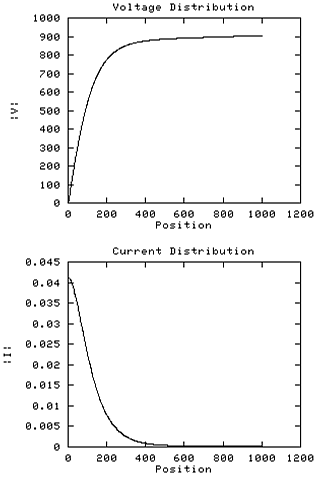 Still with longitudinal coupling switched off, we now attempt to
exaggerate the effect of external capacitance by
introducing an artifical Cext profile based on an exponential
decay factor of 0.33 for each of 32 steps along the coil. This represents a
much steeper decay of Cext than is normally found,
with the distribution heavily biased towards the base.
Still with longitudinal coupling switched off, we now attempt to
exaggerate the effect of external capacitance by
introducing an artifical Cext profile based on an exponential
decay factor of 0.33 for each of 32 steps along the coil. This represents a
much steeper decay of Cext than is normally found,
with the distribution heavily biased towards the base.
The voltage profile is now significantly altered, achieving 90% of
the final voltage in the first 20% of the coil. The current decays
equally rapidly, and the proportionality between I(x) and dV(x)/dx
is clear to see.
The transimpedance is a mere 22K ohms, demonstrating the poor utilisation
of the coil in this extreme base-heavy external capacitance configuration.
Clearly, to prevent excessive stress near the base of the coil the
geometry should introduce as little external capacitance as possible
in this region.
| Example 6: With spot external capacitance |
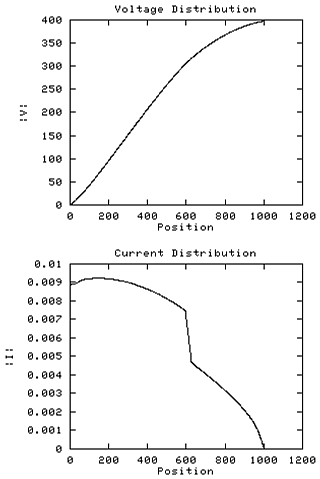 We now return to the fully modeled coil with longitudinal coupling
restored.
We now return to the fully modeled coil with longitudinal coupling
restored.
This example shows the effect of a lumped external capacitance of 10pF
applied at turn 625. This might be typical of an applied voltage probe.
The sharp fall in current at the point of application is prominent,
starving the upper portion of the coil of current, and causing a
slight convex knee in the voltage profile as dV(x)/dx is suddenly
reduced. Above and below the capacitance impulse the current
profile has the same shape as the unaffected coil.
| Example 7: No external capacitance |
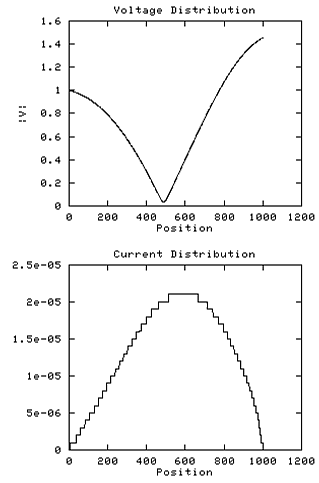 This simulation is of the normal coil with longitudinal coupling
but with virtualy no external capacitance, as might be obtained
by a coil operating far removed from other objects (*).
This simulation is of the normal coil with longitudinal coupling
but with virtualy no external capacitance, as might be obtained
by a coil operating far removed from other objects (*).
The linear-V weighted internal capacitance remains 1.98pF.
The reader will recognise this as a half wave resonance and this
is the lowest mode available to the coil in the absence of an
external current path.
This configuration is of interest because it presents the
minimum possible capacitance to the resonator, and thus maximises
the ratio of end-end voltage to stored energy for a given coil.
When referenced to the potential at one end, the half wave voltage
profile is a distorted sine, appearing concave in the lower half and
convex in the upper half.
The current profile is particularly interesting, as it is enforced
by the largely symmetric internal capacitance distribution.
There is no longer any external
capacitance displacement current to break the symmetry. This mode
represents the 'groundstate' resonance of a free coil.
(*) A small amount of Cext must remain to provide a
return path for the simulator to energise the coil through the base.
These profile charts refer to operation just below the resonant frequency,
since tsim is not configured to explore the even-wave modes
properly.
The quantisation is caused by limited output file precision in tsim.
| Example 8: Typical coil with toroid |
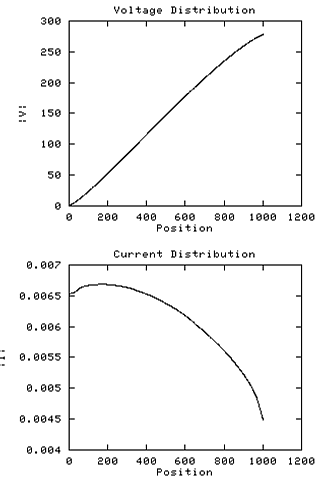 The same fully modeled coil as in example 1, but this time with a toroid
applied, contributing around 25pF of topload. With this geometry the
linear-V weighted equivalent internal and external capacitances are now
1.91pF and 8.49pF. As usual the toroid, by its shielding effect on the
coil, has stolen some of the coil's Cext.
The same fully modeled coil as in example 1, but this time with a toroid
applied, contributing around 25pF of topload. With this geometry the
linear-V weighted equivalent internal and external capacitances are now
1.91pF and 8.49pF. As usual the toroid, by its shielding effect on the
coil, has stolen some of the coil's Cext.
The non-zero current at the top of the coil is
apparent and its value of 4.5mA is consistent with the top voltage of
278 volts into a 25pF capacitance.
The transimpedance is 43K ohms, much higher than the 29K predicted
by a cosine current profile, and almost equal to the uniform current
value of 45K ohms.
The voltage profile now remains more linear over the whole length
of the coil, and the input impedance is significantly lower than that
of the unloaded coil.
| Example 9: With small external capacitance and small top load |
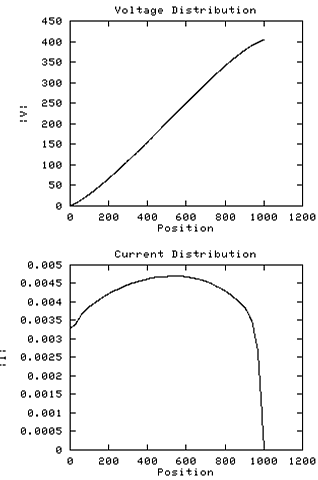 The coil is high off the ground so that Cext is about a quarter
of its normal value. A small top loading capacitance of about 5pF is
applied to the top of the coil.
The coil is high off the ground so that Cext is about a quarter
of its normal value. A small top loading capacitance of about 5pF is
applied to the top of the coil.
The result is a largely uniform current distribution all along the coil,
and a fairly linear rise in V.
This external capacitance configuration can also be brought about by
inverting the resonator, ie
treating the top of the coil as the grounded end through which the drive is
applied, and the coil base is then the open circuit hot end.
Transimpedance is very high under these conditions, 122K ohms, since
maximum use is being made of the inductance. In fact the transimpedance
prediction based on uniform current is only 95K ohms, and the extra
impedance appears to be due to circulating currents in the internal
capacitance, as hinted at by the hump in the current profile.
The current peak at 15% height which was starting to appear
in example 1 has enlarged and moved almost to the half way point on the coil.
Thus we
seem to get more than our money's worth out of the coil in this
configuration.
Note that due to this current hump, there is a very slight concavity
in the lower half of the V profile, and a corresponding convexity
in the upper half.
This configuration is worthy of further study as it highlights the extra
peculiarities of the transmission line in the presence of longitudinal
coupling.
We would expect a normal
(non-inverted) Tesla coil fitted with a large topload to approach these
profiles in the absence of a nearby ground plane. The action of the
internal capacitance is probably responsible for the
good performance reported in these cases.
| Example 10: Inverted capacitance distribution |
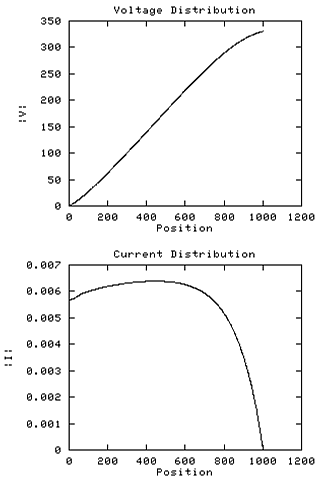 This time the fully modeled coil, without a toroid, is subjected to an
artificial external capacitance distribution generated by an exponential
decay factor of 0.2 for each of 32 steps, but starting from the top end,
in other words, the maximum Cext is at the top.
This time the fully modeled coil, without a toroid, is subjected to an
artificial external capacitance distribution generated by an exponential
decay factor of 0.2 for each of 32 steps, but starting from the top end,
in other words, the maximum Cext is at the top.
The current profile is almost uniform along 80% of the coil, falling
rapidly beyond this point.
This configuration is similar to the previous example
except that in this case the external capacitance is quite high.
It is heavily biased towards the top and we are just beginning to
see the formation of the midpoint current hump.
The transimpedance is 58K, so clearly the ability of the coil to
raise a top voltage is not upset by this inversion of the normal
Cext distribution. While this situation may therefore
be advantageous to a CW coil, a capacitor discharge system will
suffer from the reduced ratio of topvolts to stored energy.
The base input impedance is about the same as that of the coil
with toroid.
| Summary |
The following notes apply only to the 1/4 wave resonance.
Mutual inductance acts to make the induced series emf at any point dependent on an average of the nearby current and therefore appears to 'smooth out' the voltage and current profiles. This longitudinal coupling acts to increase the velocity slightly and can be thought of as a 'stiffening' of the coil. This velocity increase is larger at higher frequencies and the effect is to reduce slightly the dispersion introduced by the internal capacitance.
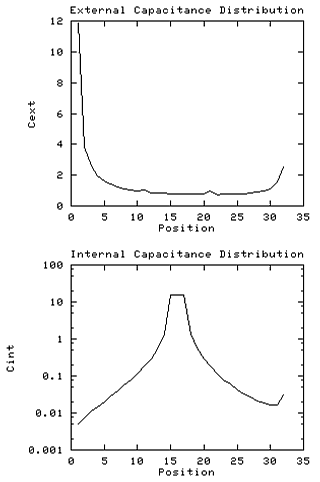
This is the major determining factor of the current distribution, the rate of decrease of current -dI(x)/dx being proportional to the external capacitance Cext at point x. End effects generally result in a bathtub shape to the distribution, as shown in this chart of the profile for Terry's coil over a ground plane without a toroid. The glitches at one-third and two-thirds height are artifacts of the tlap program which calculated the profile.
Displacement currents through this charge storage mechanism act with the
external capacitance in the top half of the coil, and against it in the
lower half. As a result,
in the lower half of the coil, dI(x)/dx can become positive in regions
where internal displacement current exceeds the external. This can cause
a slight current peak near the bottom of the coil. When the external
capacitance is reduced, the effect of Cint becomes more
noticeable and the current peak moves up the coil towards the midpoint.
Currents circulating through Cint can
cause the transimpedance to exceed that of a coil with uniform current.
The chart shows the distribution of internal capacitance between a point in the
middle of the coil and the rest of the coil. The flat top is due to
limited spatial resolution in the tlap laplace solver program
from which these distributions were obtained.
Internal capacitance reduces the velocity and the reduction is greater
at higher frequencies, causing dispersion, and this is the main cause of the
non-harmonic relationship of the overtones to the fundamental resonance.
These are always monotonically increasing, since to do otherwise would require a phase reversal of current coinciding with a voltage turning point, which is inconsistent with the quarter wave resonance. The shape of the V profile lies between a linear rise and a sine rise, and when internal capacitance effects are prominent, a slight concavity occurs in the lower half and a corresponding convexity in the upper half, thus forming a point of inflection coinciding with the current peak. In the absence of internal capacitance the dV(x)/dx has to be monotonically decreasing.
These lie somewhere between a uniform and a distorted cosine profile, determined mainly by the Cext distribution and the amount of top loading. The current profile would be forced to be monotonically decreasing if it were not for the circulating action of the internal capacitance. There can be no zeroes of the current profile within the coil as this would require a phase reversal. A peak in the current (due to Cint) will cause a corresponding point of inflection in the voltage profile. Configurations involving minimum distributed external capacitance result in maximum ratio of Vt to stored energy for any given coil, and addition of top load improves the utilisation of the coil as described by its transimpedance.
For explanation of terms used above, see pn2511 - Secondary Basics.