We consider all types of secondary shape: flat, cylinder, and both inverted and upright cone coils. To do so we define two shape parameters A and B to describe each coil:

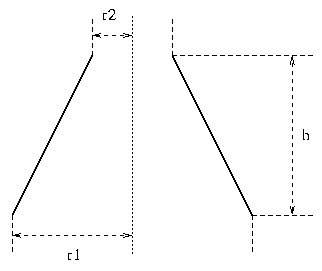
Starting with the definitions shown on the right, in which r1 is the radius across the lower (earthed) end of the coil, and r2 is the radius across the upper (hot) end, we define: A = h/d B = (r1 - r2)/d where h = overall height of the coil. and d = average diameter = r1 + r2. Thus A is the familiar h/d ratio with A=0 corresponding to a flat spiral coil. The factor B describes the tilt of the sides of the coil, and is zero for a cylindrical solenoid. A cone coil which rises to a point at the top has B=1 and an inverted pointed cone balanced on its point has B=-1. Shapes with A=0 range from B=1 corresponding to a full spiral with center hot, to B=-1 corresponding to the full rim-hot spiral. The shape with A=0 and B=0 corresponds to a coil with all the turns bunched into an annular ring.

We show the ratio Les/Ldc as a function of the shape parameters A and B. The ratio varies with the height of the coil above ground, so we present two tables. The first is calculated for coils whose base is raised off the ground by twice the coil's average diameter. The second is for coils where the base is raised by only half the average diameter.

Both tables apply only to unloaded secondaries and an adjustment to the table ratio must be computed when dealing with toploaded coils.

The ratio Les/Ldc increases rapidly as A and B both tend to zero. For this reason the cell A=0, B=0 is left empty and this cell would require expansion to a sub-table in order to carry any useful detail.

Each of the table values is an average of around 6 coils spanning a wide range of turns and sizes normally used for Tesla coils. The overall variation of the ratio Les/Ldc within each cell is only about 0.5%, which demonstrates that this inductance ratio is mainly determined by the overall shape of the coil, rather than by size or detail of winding. This is because the inductance ratio is derived from the current profile, which in turn is determined by the distribution of capacitance along the coil. Short coils, in which internal capacitance dominates, tend to have an inductance ratio greater than unity. Similarly, raising the coil clear of the ground increases the proportion of internal capacitance, thereby increasing the ratio.

High elevation coils: base = 2 * d above ground
B
A		-1.0	-0.8	-0.5	-0.3	0.0	0.3	0.5	0.8	1.0
	0:	1.19	1.20	1.27	1.40		1.63	1.48	1.38	1.36
	1.0:	1.17	1.15	1.14	1.14	1.15	1.17	1.18	1.23	1.23
	1.5:	1.13	1.11	1.08	1.06	1.04	1.06	1.09	1.14	1.18
	2:	1.10	1.08	1.03	1.00	0.98	0.99	1.02	1.08	1.12
	2.5:	1.08	1.04	0.99	0.95	0.93	0.95	0.98	1.04	1.07
	3:	1.05	1.02	0.95	0.92	0.90	0.92	0.95	1.00	1.04
	4:	1.01	0.97	0.90	0.87	0.85	0.87	0.90	0.96	0.99
	6:	0.95	0.91	0.84	0.82	0.81	0.83	0.86	0.91	0.93
	8:	0.90	0.87	0.80	0.78	0.77	0.81	0.84	0.88	0.90
	10:	0.87	0.84	0.78	0.76	0.76	0.79	0.82	0.87	0.89

Low elevation coils: base = 0.5 * d above ground
B
A		-1.0	-0.8	-0.5	-0.3	0.0	0.3	0.5	0.8	1.0
	0:	0.99	1.01	1.08	1.19		1.29	1.13	1.01	0.98
	1.0:	1.06	1.06	1.05	1.04	1.03	1.03	1.01	1.01	1.01
	1.5:	1.06	1.04	1.00	0.98	0.95	0.95	0.95	0.97	0.97
	2:	1.05	1.01	0.96	0.93	0.90	0.90	0.91	0.93	0.95
	2.5:	1.03	0.99	0.93	0.89	0.87	0.87	0.88	0.91	0.93
	3:	1.01	0.97	0.90	0.87	0.84	0.84	0.86	0.89	0.91
	4:	0.98	0.93	0.87	0.83	0.80	0.82	0.84	0.87	0.89
	6:	0.92	0.88	0.82	0.79	0.77	0.79	0.81	0.84	0.86
	8:	0.89	0.85	0.78	0.75	0.75	0.77	0.80	0.83	0.85
	10:	0.86	0.82	0.76	0.74	0.73	0.76	0.79	0.83	0.84

The tables were generated using Terry Fritz's Sun workstation as a byproduct of the secondary gradient factor tabulation.