Intro

The direct turn-to-turn capacitance makes a small and usually negligible contribution to the overall effective reactances of typical primary and secondary coils. But a primary design involving a wide compact spiral ribbon exhibits a particularly large turn-to-turn capacitance, and the question is - can we still ignore it when making design calculations?

Chris Swinson wrote:

> my primary will be 4 turns of 2" wide strap separated
> about 1mm apart.. the dia is about 22"

This particular coil is a good candidate for discussion, and the topic is worth pursuing due to the evolving requirements for lower impedance primary windings demanded by some of the modern TC designs.

It turns out that the turn-to-turn capacitance here has a very large effect on the self resonance of the coil compared with a wire coil of the same dimensions and turns. When this primary coil is resonated with a primary capacitor, the change in the resonant frequency is much less, but could still be significant in precision coil design and modelling.

The lowering of the resonant frequency due to this inter-turn capacitance occurs by increasing the effective inductance of the coil, an increase which comes about as a result of circulating currents raised within the coil - currents which pass through the inter-turn capacitance.

These notes describe in some detail just how this occurs, and explains why it is the inductance that alters and not the resonator's capacitance. A spice model of the coil is used to demonstrate the modelling principles and to estimate the effective parameters of this coil.

Some concepts will have to be introduced which may not be familiar to coilers who have not delved into the finer details of modelling distributed resonators, and it is hoped these notes will make an interesting introduction to the subject.

Internal and External Capacitance

It is necessary to distinguish between two types of self capacitance which occur in a coil. The term 'self capacitance' is often used casually in discussions, but here we need to be a little more precise and recognise the difference between the internal and external capacitance of the coil.

The external capacitance is the one which tends to be visualised by coilers. It involves lines of the E-field leaving the coil and terminating somewhere in the surroundings. By contrast, the internal capacitance accounts for E-field flux lines which leave one part of the coil and terminate on another.

The important distinction between internal and external - and the reason we do in fact bother to separate them - is that only current passing through the external capacitance (plus any load current) eventually returns back to the source. The total current through external capacitance (plus the load current) equals the base or drive current.

Note, we are picturing coils here with one end grounded and the other, the 'hot' end, either open, or loaded by a tank or toroid capacitance. Later we will model some coils and for modelling purposes we will excite the resonator with a current source inserted between the 'cold' end of the coil and ground. This current source, therefore, carries the total current through the external capacitance of the coil and load.

In contrast, current passing through the internal capacitance of the coil does not leave the coil, and is invisible to the external circuit and our current source. It makes itself felt, as we shall see, by modifying the effective inductance of the coil at frequencies where significant current passes through the internal capacitance.

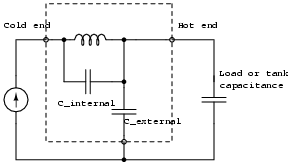
A lumped circuit which helps to visualise the two types of self capacitance. The current source feeds current into the coil, which eventually returns via either the external self capacitance or via the load/tank capacitor. Current through the internal capacitance is not accessible to the external circuit.

In most coils (secondary and primary), the internal capacitance does not affect the coil parameters very much. For example, in a typical secondary coil, the effective inductance at the operating frequency might be increased by 5 to 10% due to internal capacitance.

The contribution of internal capacitance does become dominant at the higher (overtone) resonances of the coil (in which an in-coil wavelength spans only a few turns), and also in very short (h/d < 1) coils and coils with multiple layers.

Turn-to-turn Capacitance

The direct capacitance between consecutive turns can be quite high in a typical primary or secondary coil, with values ranging from 20pF to 200pF per turn. However, the contribution of this turn-to-turn capacitance to the overall effective reactance of the coil turns out to be quite small for typical solenoid and spiral coils.

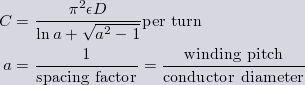
The palermo formula calculates the turn-to-turn capacitance of a pair of turns of diameter D. Epsilon is the absolute permittivity of whatever material fills the space between the conductors. It applies only to wire conductors of round cross section.

This limited effect occurs because the inter-turn voltage is generaly only a small fraction (about 1/N in an N turn coil), of the total coil voltage. Turns further apart also have a mutual capacitance between them, which is much lower of course, but the voltage between each pair of these 'remote' turns is higher, and there are about N-squared/2 pairs of these mutual capacitances all contributing to the internal capacitance. In the end, the remote turns dominate in the coils we normally use and as a result, the internal capacitance tends to be governed by the overall geometry of the coil, rather than the direct inter-winding capacitance.

The turn-to-turn capacitance contributes about 10% to the total internal capacitance, but this internal capacitance itself affects the resonant frequency only about 5%. We usually then neglect the inter-turn capacitance when constructing models of the coil's reactances.

The above reasoning applies to 'normal' coils which we have frequently measured and modelled to confirm these statements. A coil made of parallel ribbon is likely to have a rather larger turn-to-turn capacitance.

Formula for the turn-to-turn capacitance between turns of a spiral ribbon coil. This is just the formula for the capacitance between parallel plates having the area of a turn - the circumference times the ribbon width.

This parallel plate formula will be applied now when we set up an approximate model of the coil's internal capacitance.

Coil Modelling

Both the internal and external capacitances, as well as the coil's inductance, are distributed along the coil and cannot be directly represented in a circuit diagram. We have to approximate these distributed reactances by segmenting the resonator into a number of pieces and lumping the inductance and capacitance of each segment. This involves an approximation, of course, but we can achieve whatever accuracy we desire by choosing to segment the resonator into larger numbers of smaller pieces.

A distributed resonator usually has many resonant frequencies, the collection of which is sometimes called the mode spectrum. The lumped equivalent circuit can only represent a certain number of these modes, that number increasing as the segmentation of the model is made finer. The worst case is segmentation into just one piece, as in the diagram above. This single LC model can only represent one resonant mode, which is often adequate. But the actual values of the lumped inductance and capacitance to be used in that single LC circuit have to be derived from a model which uses a finer segmentation if the model is to accurately represent operation at the single resonant mode.

For easy visualisation, we will segment this four-turn coil into four segments, ie one segment per turn.

Internal Capacitance

For the coil under discussion, its 56cm diameter and 1mm spacing produce turn-to-turn capacitance of about 780pF. Added to this are the longer range contributions, of which there are N * (N-1)/2 - N + 1 pairs of mutual capacitances in an N turn coil. For this coil, that's only 3 more! We can even itemise them!

Only the edges of the ribbon act as electrodes for the longer range internal capacitances, so we can model these terms as if they were thin wires and use a capacitance extraction program to determine their values for each pair of turns.

 Pair 1:  2 turns gap  4.8pF
 Pair 2:  3 turns gap  4.7pF 
 Pair 3:  2 turns gap  4.8pF

The three inter-turn capacitances of 780pF plus the three longer range internal capacitances listed above might be represented in a circuit model thus:-

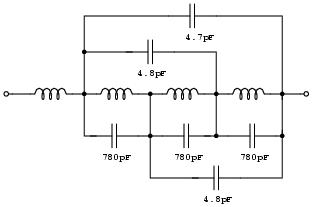
This is just one way to approximate the distributed internal capacitances in a lumpy turn-by-turn model. There is some leeway over just where you choose to hang the capacitances.

It seems likely that in this extreme coil we cannot off-hand disregard the turn-to-turn capacitance as we do in a more typical coil. In fact, the inter-turn capacitance dominates the internal capacitance of this coil.

A Network Model

To complete this simple four-segment model we have to add on the external capacitances - that is, the distributed capacitance between each segment of the coil and the grounded surroundings.

Some further capacitance extraction gives some external capacitance samples which are added here to the model.

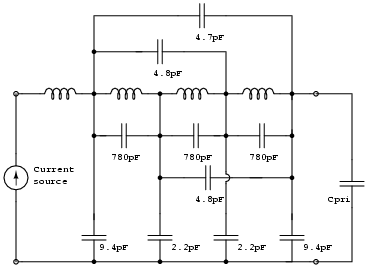
The network model with external capacitance added. These values are only qualitative and the external capacitance in reality would vary somewhat with the coil's relationship to its surroundings. The two 'inside' turns are only contributing 2.2pF each. The exposed surfaces of the inner and outer turns add a little more. The 'load' in this case is the primary tank Cpri attached to the 'hot' end of the coil on the right, and imagine a drive source applied to the left hand terminals.

This network model is not quite in a fit state to present to a circuit simulation program, we need to do a little more work to establish a value for the four inductances shown in the diagram, which are the self inductances of each turn. Also, not shown in this diagram, are the mutual inductances between each turn, which are very important. Later we will describe how these are constructed, but for now we will continue to discuss the capacitances.

Cdc - DC or Low Frequency Capacitance

Apply a constant DC voltage to the input terminals. All the internal capacitances are shorted by coils, and all the external capacitances and Cpri are charged up to the source voltage.

In this statically charged condition, the total stored charge is equivalent to that of a single capacitance equal to the parallel combination of all the external and load capacitances - in this case 23.2pF + Cpri. This we define as the Cdc of the resonator, and the Cdc due to the coil alone is 23.2pF.

This quantity can be measured directly simply by connecing a capacitance meter to the coil - so long as the operating frequency of the meter is much lower than the lowest resonant frequency of the coil. This direct measurement of Cdc can be a useful cross check on the extracted values of the external capacitance.

Ces - Equivalent Shunt Capacitance

Imagine now an AC drive signal set to the lowest resonance of the network - the fundamental. In this mode of resonance, all the circuit voltages are in phase - meaning - they all waggle up and down in unison. Also, assume that the induced voltage across each turn is the same, or in other words, a linear voltage rise exists along the winding. This will be the case, approximately, because of the mutual coupling between the compact turns, as will be seen later. Let this voltage per turn be Vt and picture the circuit 'frozen' at an instant in the AC cycle in which all the coil currents are momentarily zero while at the same time, Vt is at a peak of its sinusoid. At this point in the oscillation, all the stored energy is held in the E-field of the coil.

Let us list all the stored charges in the system, on the basis of Q = CV for each of the 11 capacitances.

  4.7 * 3Vt * 1 cap   (int)
  4.8 * 2Vt * 2 caps  (int)
780.0 * 1Vt * 3 caps  (int)
  9.4 * 1Vt * 1 cap   (ext)
  2.2 * 2Vt * 1 cap   (ext)
  2.2 * 3Vt * 1 cap   (ext)
  9.4 * 4Vt * 1 cap   (ext)
 Cpri * 4Vt * 1 cap   (Cpri)

It is important to remember now that only the external capacitances and Cpri have their charge displacements supplied directly from the drive loop. The total charge supplied by our current source to set up this linear voltage distribution is therefore the sum of all the external and Cpri charges, ie

   Vt * (9.4 * 1 + 2.2 * 2 + 2.2 * 3 + 9.4 * 4 + Cpri * 4)

which comes out to Vt * (58.0 + 4 * Cpri). In terms of the displacement current supplied by the drive, this is equivalent to a single cap of 14pF + Cpri charged to the hot-end voltage, 4Vt. This reduces the coil (as far as the drive circuit is concerned) to the equivalent circuit given below.

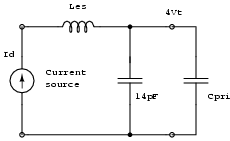
The effective capacitance of the resonator as seen by the driver operating at the fundamental resonant mode. The inductance shown here is not the low frequency inductance of the coil, but is an effective value, valid only near the resonant mode, which is discussed later.

We define the 14pF to be the equivalent shunt capacitance Ces of the coil when at (the fundamental) resonance. And 14pF + Cpri is the Ces of the resonator as a whole. The Ces is important because the following equations apply.

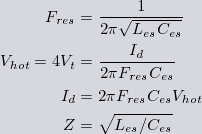
Familiar equations for a lumped LC resonator. But the values of L and C employed here are not the 'low frequency' values, but are 'equivalent' values calculated to take account of the non-uniform distribution of current and voltage in the coil.

Note that the large internal capacitance is apparently invisible to the driver and it may seem that the internal capacitance has been disposed of altogether, as it doesn't contribute at all to the external drive current or the effective shunt capacitance. But this is far from the case and we are only half way through the story. It turns out that, from the point of view of the driver, the internal capacitance manifests itself in the value of the effective inductance, Les. To understand this we have to digress now to discuss the inductance of the coil.

Ldc - Low Frequency Inductance

To begin a clear picture of the coil's inductance we must first look at how the total induced voltage is obtained in a coil from the induction in each turn.

Each of the N turns of the coil has a self inductance, as well as a mutual inductance with every other turn of the coil. With a current at low frequency passing through the coil, and all the turns therefore carrying the same current, the total induced voltage is proportional to the sum of the N self inductance terms, plus the N * (N-1) mutual inductances. The low frequency inductance of the coil as a whole is therefore the straight sum of all the self and mutual components arising from the individual turns (or whatever other unit of segmentation you care to break the coil into). This defines the low frequency inductance Ldc, which is the inductance obtained by all the various inductance formulae such as Wheeler or Lundin.

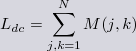
	The low frequency inductance of the coil modelled in N segments is just the sum of all the mutual and self-inductance contributions. Here M(i,i) is the self inductance of the turn labelled i, and M(i, j) is the mutual inductance between turns i and j.
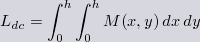
	As the number of segments N is increased to an infinite number of infinitesimal segments, the discrete sum above turns into a continuous integral and M becomes a function of two continuous position variables.

You must remember, the key feature of Ldc is that it only applies to the coil when all the turns carry the same current.

Inductance of a compact coil

In this type of compact coil, all the turns are fairly close to one another and therefore largely intercept the same magnetic field, and consequently all have approximately the same induced voltage. In other words, in a compact coil the self inductances of all the turns, and all pairs of mutual inductances between turns, all have the same value.

This means that the elements of the matrix M of mutual and self inductances of the turns are all the same value. Lets call this value Lt - the self inductance of a turn. Then, for a compact coil we have a simple relationship between the inductance of a turn and that of the coil as a whole.

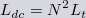
For a compact coil where all the turns intercept pretty much the same magnetic field, all the self and mutual inductance coefficients are equal to the self inductance Lt of a turn. N-squared of these inductances all add to give Ldc.

Remember, this only applies to a compact coil in which all the turns are closely coupled to one another. In a longer coil such as a solenoid, the mutual coupling coefficients decay with the separation of remote turns and thus the total inductance has to include a geometry factor, called the Nagaoka coefficient, determined from the shape of the coil. In our case, this coefficient is close to unity.

To find Lt for a compact coil, you can use, say, a Wheeler formula, for the coil as a whole and divide the answer by N-squared. Or you can apply a formula directly for the self inductance of a turn. You can gauge the error in this 'compact' approximation by comparing the two answers.

We will treat the flat spiral primary under discussion here as a 'compact' coil. With the dimensions given, the total Ldc of the coil will be about 19uH, so that the each of the 4 turns, and all 6 distinct pairs of mutual inductances all have the value Lt = 1.2uH.

Les - Effective Series Inductance

At high frequency the current, as we shall see, is no longer uniform and the result is that the coil does not develop the same induced voltage (for a given input current) as it did at low frequency. In other words the apparent inductance of the coil will be different from Ldc.

For the moment, pretend there is no internal capacitance at all, and that only the external capacitance is present, plus perhaps a Cpri at the 'hot' end of the coil.

Current into the first turn will equal the drive current Id. Current into the second turn will be that of the first turn, minus the current diverted into external capacitance by that point. Likewise, after the next turn, a little more current has been shunted to ground via external capacitance. Describing the same thing from the viewpoint of the charges themselves, some of the charge entering the coil gets 'hung up' along the way in order to do the job of placing the coil's induced voltage distribution across the external self capacitance.

The end result is the current leaving the coil into Cpri is less than the current Id entering the coil from the driver. In other words, the coil current is no longer uniform. The significant consequence of this is that the total induced voltage is less than would be obtained by an inductance of Ldc, because turns further from the drive are not carrying the full current and therefore not contributing quite as much to the total induced voltage. This appears to the external circuit as if the coil has an effective series inductance, Les, somewhat less than Ldc.

In a regular secondary solenoid, the reduction of inductance due to this might be 30% for an unloaded coil and maybe only 5 or 10% for a toploaded coil. Observe that the higher the load current is compared with the current diverted into the distributed external capacitance, the more uniform will be the coil current, and therefore the closer Les will be to Ldc.

Well, that's the picture in the absence of any internal capacitance.

Les and internal capacitance

We reintroduce the internal capacitances and return to the 'frozen' view of the circuit described earlier, in which all currents are momentarily zero and the voltages across all the capacitances are at their peak. We can see that at this instant the internal capacitances are all charged up by the induced voltages across the turns of the coil which they span.

Now consider the fate of this 'internal' stored charge as the resonator moves through the next quarter-cycle of oscillation. At the end of this quarter-cycle, the H-field is now at a maximum and the E-field has collapsed. In other words, the coil current is now at a maximum and all the capacitances, internal and external and Cpri, are completely discharged. Now we have already seen that the only charge which the driver sees is that which passes through the external capacitance. Therefore the internal capacitances will have discharged through the turns of the coil, and as a result, will have increased the total induced voltage over and above that which was being produced when we only had the external capacitance. The 'hot' end voltage is now higher, then, for the same input coil current Id, than it was without the internal capacitance. In other words, the effective inductance has been increased by putting in the internal capacitances.

A very rough idea of the amount of extra induction can be obtained as follows. Let the dominant inter-turn capacitance be Ct, in this case 780pF. For a turn-to-turn voltage of Vt, the charge across each inter-winding capacitance is Qt = Ct * Vt and this discharges into a turn with a peak current of 2pi * F * Ct * Vt The original peak coil current, with just external capacitance, would have been 2pi * F * Ces * 4Vt. Therefore, the current has internally increased by a factor of roughly 1 + (Ct / 4Ces), which for our coil comes out to about a factor of 15. The result is that the coil induces about 15 times the voltage for a given input current than it would do without the internal current caused by the turn-to-turn capacitance! Effectively the self inductance has gone up by a factor of fifteen as far as the external circuit is concerned, and the resonant frequency will be lowered by a factor of almost four.

Circulating currents and current distribution

We can broadly picture the internal capacitance in terms of loops of currents 'circulating' within the coil itself, passing through the turns as conduction current and closing their loops via the displacement current of the internal capacitance. The overall effect, as far as the outside world is concerned, is to increase the effective inductance of the coil. One can think of the 'top' voltage of the coil, ie that across Cpri, as induced through the sum of the straight-through current (to Cpri) and shunt external C current, (both of which the driver sees in Id), plus a further voltage induced by the action of circulating currents within the coil (which the driver does not see).

When we only had the external capacitance, the coil current was highest at the input, equal to the drive current Id, and everywhere else in the coil, the current was less. The Les was therefore always less than the uniform current inductance Ldc. But now that we have allowed the internal circulating currents to come into play, the current within the coil will be larger (in places) than the input current. In other words, the location of maximum current has been shifted from the input of the coil to somewhere within the coil. The effective inductance Les is now able to exceed the low frequency inductance Ldc, and will do so if the total contribution to induced voltage due to the internal loops exceeds the reduction of induced voltage resulting from diversion of current into external capacitance.

Thus we can expect to find that in some coils - those where internal capacitance is significant - the effective series inductance, Les, will be larger than Ldc. In fact, this happens for solenoid coils of less than about unity h/d ratio, and almost always occurs in flat spiral coils. See TSSP: Equivalent Series Inductance for a tabulation of the ratio Les/Ldc for a range of coil geometries. In that table, flat spiral coils correspond to the row A = 0, and solenoid coils correspond to the column B = 0. All the others are conical coils of one shape or another. The compact ribbon coil under discussion has A = 0 and a B value of around 0.1 or less, so we can see from the table that Les is going to be more than 40% higher than Ldc purely due to its geometry, and the presence of the large turn-to-turn capacitance is only going to increase that percentage.

Remember that these ratios are all calculated for an unloaded coil. The addition of a 'hot' end load such as Cpri will set up a straight through uniform component to the coil current which will bring the value of Les back down towards Ldc.

Incidentally, as the 'internal' contribution to Les is increased by making the coil more compact, the location of the current maximum moves towards the center of the coil, and the magnitude of the current max, compared with the input current, increases. In extreme cases, virtually all of the resonating current is 'internal' and hardly any of it is looping out through the drive circuit, and the resulting current distribution looks more like that of a half-wave resonator - a small current at the ends and a large current in the middle.

You can describe this in terms of a coupling coefficient. With no internal capacitance, all of the circulating current of the coil passes through the driver - the drive source is coupled to the resonator with unity coefficient. As internal capacitance takes effect, only part of the the coil's resonating current passes through the driver and the coupling coefficient is less than unity.

Modelling the Coil

There are two phases to modelling a coil. The first is to determine the distributed reactances and represent these in terms of lumped self and mutual reactances between the segments into which the coil is decomposed. The second phase is to model the resulting network of L, C and M to determine the resonant frequencies, voltage and current distributions, equivalent reactances Les and Ces, transfer (surge) impedances, and so on.

The first phase - the determination of the physical reactances, has already been done and the approximate values were shown earlier in the equivalent network for the coil. We will assume that Ldc is 19uH and that a 'compact' approximation is valid so that all the L and M terms are equal to 1.2uH. We can now construct a spice model, based on the earlier network but including all 6 pairs of mutual inductance by putting in a coupling coefficient of unity between all pairs of the four turns.

Compact Spiral Primary - Test 1
.OPTIONS NOMOD NOPAGE CHGTOL=1e-16

.OP
.AC LIN 10000 100K 20000K

L1 N1 N2R 1.2e-6
R1 N2R N2 0.1
L2 N2 N3R 1.2e-6
R2 N3R N3 0.1
L3 N3 N4R 1.2e-6
R3 N4R N4 0.1
L4 N4 N5R 1.2e-6
R4 N5R N5 0.1

C1 N2 0 9.4e-12
C2 N3 0 2.2e-12
C3 N4 0 2.2e-12
C4 N5 0 9.4e-12

C5 N2 N3 780e-12
C6 N3 N4 780e-12
C7 N4 N5 780e-12
C8 N3 N5 4.8e-12
C9 N2 N4 4.8e-12
C10 N2 N5 4.7e-12

K12 L1 L2 1.0
K13 L1 L3 1.0
K14 L1 L4 1.0
K23 L2 L3 1.0
K24 L2 L4 1.0
K34 L3 L4 1.0

RL N5 0 1e12
IS N1 0 DC 0 AC 1

.PRINT AC V(N1) V(N5)
.END

This spice model is the basis for the following simulations.

Simulation results - unloaded coil

We will model the coil both with and without the internal capacitance in order to demonstrate its effect.

The increase in effective inductance when the internal capacitance is put in is dramatic - a factor of nearly 14 - which we were expecting from our rough estimate earlier.

Note that Les without internal capacitance is somewhat lower than the low frequency inductance Ldc of 19uH, also as expected.

The reader will hopefully appreciate by now the importance of attributing the reduction of resonant frequency to an increase in effective inductance. A more naive approach, which might have simply assumed that the internal capacitance adds to the effective capacitance, would have seen a reduction in frequency alright, but would have dramatically underestimated the surge impedance sqrt(Les/Ces) of the coil and so would seriously have underestimated the output voltage as a consequence.

Simulation results - loaded coil

The above simulation was applied to the open-ended coil. We now add a primary capacitor to simulate a realistic primary tuning. For the sake of argument we will use a 3nF primary tank capacitor, and repeat the above set of simulations. The tank capacitor is represented by an additional statement CPRI N5 0 3e-9 in the spice model.

Now that the coil is loaded by a typical tank capacitor, the coil current is substantially uniform and the effective inductance is no longer raised by an extreme factor. We would not lose much accuracy if we left out internal capacitance between turns, nor in fact, would we lose much more accuracy if we left out the coil's self capacitance altogether, as is normally the case when primary coils are designed and modelled. With a tank capacitor of this size, even the extra large capacitance between consecutive turns of the ribbon conductor can probably be neglected.

Summary

• The coil's external C adds to the effective capacitance (weighted by the coil's voltage distribution), and lowers the resonant frequency;
• The coil's internal C causes circulating current within the coil which raises the effective inductance (weighted by the coil's current distribution), and lowers the resonant frequency;

• The effective capacitance Ces of the coil is given (and measured directly) by
    Id/(2pi * F * Vpri)
  where Id is the drive current and Vpri is the voltage across the 'hot' end of the coil;
• The effective inductance Les of the coil is given (and measured) by
    Vpri/(2pi * F * Id);
  
• And of course, F = 1/(2pi * sqrt( Les * Ces)) and Vpri/Id = sqrt( Les/Ces);

The above are our definitions of the effective reactances.

We can make the following conclusions from this modelling exercise,

• The turn-to-turn C may be important in compact coils, when the number of turns is small and the turn-to-turn capacitance is large due to the use of ribbon conductors. In such coils, turn-to-turn capacitance may dominate the internal capacitance.
• When such a coil is lightly loaded, large circulating currents passing through the internal capacitance can raise the effective inductance, and thus also the output voltage, by a very large factor.
• When loaded with a suitably large tank capacitor, the more uniform coil current brings the effective inductance down to only a little above Ldc.
• The circulating current is still there when the coil is loaded, but it is now much smaller in proportion to the total coil current.

It is hoped that while estimating the effect of turn-to-turn capacitance in this unusual primary coil, we have shed a little light on the modelling process and clarified the often confusing concepts of distributed and equivalent lumped self-reactances. If you want to read more about the physics of resonant coils, visit the TSSP project's website. The self reactances of the coil are described in a little more detail (and a bit more math) in pn2511, and for the determined reader, the distributed resonance is described in terms of integral operators in a work-in-progress, pn1401.