Notes on Operation and Performance

The decoder operation is described in detail in the Technical notes and is just summarised here:

• The decoder makes its best guess of the carrier reference phase by squaring the entire signal. This maps both symbol phases to the same phase and the squared signal is measured in the narrow bandwidth of the inverse message duration to obtain a reference phase modulo 180 degrees;
• The decoder runs a phase search which involves multiple runs of the Viterbi list decoder. The phase search starts with the estimated reference phase and gradually moves further away;
• As the phase search proceeds, the decoder retains the result which has the overall highest path metric. This corresponds to the codeword which has the highest correlation with the received signal;
• The outcome of the decode attempt is the surviving decoder result (if any);
• The list decoder uses redundancy in the Viterbi payload to choose which of the Viterbi outputs to accept. The CRC bits contribute directly to redundancy and there are a further 0.3 bits per character of redundancy due to the source coding which contribute in a more complicated way.

Outcomes

There are three possible outcomes of a decode attempt:

• SUCCESS. The final result of the decode attempt is the correct message;
• FALSE. The final result of the attempt is a false decode. This is a message which has a valid CRC and source coding, but is not the one that was sent;
• FAIL. The decode attempt fails to find a valid message;

The decoder itself is unable to distinguish between SUCCESS and FALSE outcomes - they can only be recognised as such by the operator or by a test script which is comparing the decoder's final result with the trial message.

Optimum list length

A decode attempt which results in a FAIL is an indication that the decoder list length is not long enough to take full advantage of the CRC and source coding redundancy. A 'deeper' search with a longer list length could have been made, which may have turned up either the correct message or a false decode. For any given amount of redundancy. increasing the decoder list length will reduce the probability of a FAIL and increase the probability of both SUCCESS and FALSE. Eventually, increasing list length will lead to negligible probability of FAIL. Increasing the list length beyond this point has no effect on the probability of SUCCESS or FALSE.

The optimum list length (for any given combination of coding, message length, and CRC size) is that which produces a negligible chance of a FAIL outcome. For the performance measurements reported in these notes, the negligible FAIL probability is defined as 0.2%. This means that increasing the list length beyond the optimum can produce no more than a further 0.2% increase in message success rate.

The optimum list length depends on the code used, the message length, the CRC size, and the phase search policy used by the decoder. It also depends to some extent on the signal/noise ratio. The table below demonstrates the typical decoder performance as the list length is increased through the optimum value.

The optimum list length in this case is somewhere between 1000 and 3000 and the decoder would choose to use 3000 to maximise the chance of a successful decode. With this setting the decoder will almost always produce a result and that result has a 56% chance of being the correct decode. The Shannon sphere packing limit for this block size is 77.6% success rate at -1.0 dB and EbNaut is performing within 0.8dB of the limit.

Trials to establish optimum list lengths make use of geometrically increasing list lengths: 1,3,10,30,100,300,... and so on. These coarse steps are reasonable because the optimum is not critical and it does not harm success rate to use a longer than optimum list length.

There is an absolute maximum list length which is reached when the list is long enough to include all possible decodes produced by the Viterbi layer. For example a one character message with 8 bit CRC has a Viterbi payload of 6 + 8 = 14 bits. There are therefore only $2^{14} = 16384$ distinct codewords and all of these will be represented in the Viterbi list if the list size is set to 16384. Increasing the list beyond this merely allocates memory which will never be used. There is no further coding gain to be obtained and a run of the decoder is equivalent to testing the correlation of the received message with all possible messages.

Optimum CRC size

If the sender chooses to use a larger CRC, then the decoder will have to use a longer list to take advantage of it. Also, sending a longer message (more characters) will introduce further redundancy due to the source coding, and a longer decoder list will be needed.

With almost all codes and message lengths, more redundancy (larger CRC, more characters) will lead to improved message success rate so long as the decoder is able to use the optimum list length for that redundancy.

Consequently, the optimum CRC size is that which has an optimum list length equal to the largest list that the decoder can use. In practice this is limited to about 3000000.

The table below shows the typical variation of performance and optimum list length as the CRC size is increased.

With short messages the CRC bits are a significant extra payload overhead for the inner convolutional code to carry. Much of the available list decoding gain is being used to compensate for this. Therefore the overall performance doesn't increase much as the CRC is increased. For example, here is the performance of a 1 character message:

The single character is encoded into 6 Viterbi payload bits, thus moving from CRC 0 to CRC 6 is doubling the convolutional code payload and therefore halving the energy per bit. All the strength of the list decoding is being used to compensate for this. This compensation continues as the CRC size is increased further and there is no overall improvement to success rate.

With longer messsages, the benefit of a larger CRC is more obvious:

The additional CRC bits represent only a small fractional increase in the Viterbi payload size and almost the full gain of the list decoding contributes to the success rate.

Phase search policy

The phase search initially tries uniform (constant throughout the message) reference phases in 30 degree steps, gradually moving further away from the initial guess obtained from the squared signal. There are 12 uniform phases to try, therefore 12 runs of the Viterbi list decoder. The decoder then splits the message into, first two parts, then four parts, and applies slightly different reference phases to each part. This involves a further 96 runs of the decoder. The intention of this stage of the phase search is to accomodate signals that are slightly off frequency or are disturbed by propagation changes such as a day/night terminator passage.

Note that it doesn't matter what order the decoder uses to trial all the variations of reference phase. The final result will be the same - the decode which gave the highest path metric (correlation). In practice the uniform phases are tried first as these usually deliver a result which will not be improved upon by further phase trials. The operator is at liberty to terminate the decode attempt at that stage.

The phase search incurs some cost in terms of coding gain. Each run of the decoder within the phase search invites the possibility of obtaining a random false decode having a higher path metric than the genuine decode, thus leading to a FALSE outcome. A consequence of this is that the optimum list length is longer if the phase search is restricted to uniform phases and this produces an associated increase in success rate. Indeed, if the phase of the received signal is known in advance (perhaps by prior carrier measurements on a repeatable path), then the phase search can be turned off and replaced by a single run of the decoder using the known reference phase. Then the optimum list becomes longer still and produces a further improvement in success rate.

An example is given in the table below:

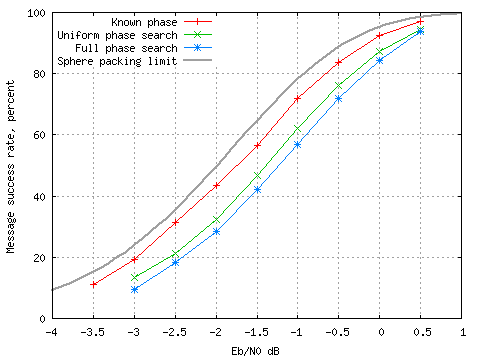
The Shannon sphere packing limit for 8K19A with 6 characters and 18 bit CRC is 78.0% at -1.0 dB and with known phase and $10^7$ list size, EbNaut performance comes within 0.25dB of the limit. For uniform phase and full phase searches, the performance is within 0.54dB and 0.72dB respectively. This gives an indication of the loss of coding gain when the reference phase has to be searched for.

The measured performance of the above code with CRC 18 over a wider range of S/N ratios is shown below:

Given a weak signal with a known reference phase, the probability of a FAIL outcome from the single run of the decoder is given approximately by $$ P(\text{FAIL}) \approx \left( 1 - \frac{1}{2^b} \right)^L $$ where $L$ is the list length and $b$ bits is the effective redundancy in the message. This formula is obtained from the probability that $L$ independent random messages from the Viterbi decoder will all fail to match the $b$ bits of redundancy. The formula is approximate because the $L$ messages being evaluated by the list decoder are not quite independent or random. The approximation is better with weaker signals.

The optimum list length (defined by 0.2% FAIL probability) for a known phase decode is therefore approximated by $$ L_\text{opt} \approx \frac{\log (0.002)}{\log \left( 1 - \frac{1}{2^b} \right)} $$

When running a uniform phase search (12 runs of the decoder in steps of 30 degrees), we might expect that the optimum list length would be $1/12^\text{th}$ of the known phase optimum. However the 12 decoder runs are not quite independent trials and there is some overlap in the results (some of the list entries found in a phase search step will also be present when running the neighbouring phases). Moving to a full phase search, the individual runs are even less independent and the optimum list length is reduced from the uniform phase optimum only by about an extra factor of $1/3$.

List decoding redundancy

The total redundancy for list decoding is $0.3$ bits per character plus the CRC size. However the effective redundancy for use in the optimum list calculation in the previous section, is often less than the total. Specifically, not all of the $0.3$ bits per character of source coding redundancy come into use on longer messages. The reason for this is that the false decodes produced by the Viterbi decoder often differ from the correct decode in only a limited number of character positions. Typically the decoder will lose the correct path through the trellis and rejoin it later after a string of incorrect bits lasting up to a few constraint lengths. Thus, many of the false decodes in the output list are incorrect only in a few characters. This limits the contribution of the source coding redundancy to the average number of incorrect characters, not the full message length.

With short messages, the false decodes usually involve errors in most or all character positions and almost the full $0.3$ bits per character are effective. The reduced redundancy becomes noticeable on messages of more than about 20 characters, and is difficult to quantify. Trials show that it depends on the constraint length of the convolutional code, the message length, and the signal/noise ratio.

In practice, for messages up to 50 characters or so, it does no harm to assume the total source coding redundancy is available. This may tend to overestimate the required list length, which does no harm to the message success rate.

Inner code performance

The performance of the inner convolutional block code for various rates and constraint lengths is shown in the table below, as a function of payload size. The payload size is calculated from 6 bits per character plus the CRC size.

Notes:

• For any given polynomial (4K19A, 8K21A, etc), performance reduces as the payload size increases;
• For payloads of 18 bits or less, there is no significant improvement when the constraint length increases beyond 19, or when the code rate is reduced;
• For payloads between 18 bits and 36 bits, there is no significant improvement beyond constraint length 21;
• For payloads between 36 bits and 72 bits, there is no significant improvement beyond constraint length 23;
• For payloads of 36 bits or more, it is worthwhile to use the lowest code rate 1/16;
• For payloads larger than 72 bits it is always worth using the longest constraint length possible (limited by decoder memory);

Performance of the inner code is reflected in the performance of the cascaded code. For example, consider a 25 character message with 12 bit CRC (Viterbi payload of 162 bits). The performance is shown in the table below, for the inner code only, and for list decoding with optimum list size for each search policy.